fig, ax = plt.subplots(3,3, sharex = True, figsize = (12,18), tight_layout=True) #
#Before Normalisation
ax[0,0].plot(T, L_nb_edges, label='Before normalisation')
ax[0,1].plot(T, L_nb_nodes, label='Before normalisation')
ax[0,2].plot(T, L_mean_degree, label='Mean degree before normalisation')
ax[0,2].plot(T, L_max_degree, label='Max degree before normalisation')
ax[1,0].plot(T, L_density, label='Before normalisation')
ax[1,1].plot(T, L_transitivity, label='Before normalisation')
ax[1,2].plot(T, L_modularity, label='Before normalisation')
ax[2,0].plot(T, L_diameter, label='Before normalisation')
ax[2,1].plot(T, L_ASPL, label='Before normalisation')
ax[2,2].plot(T, L_mean_viewer, label='Mean # of viewers before normalisation')
ax[2,2].plot(T, L_max_viewer, label='Max # of viewers before normalisation')
#After normalisation
ax[0,0].plot(T, L_nb_edges_2, label='After normalisation')
ax[0,1].plot(T, L_nb_nodes_2, label='After normalisation')
ax[0,2].plot(T, L_mean_degree_2, label='Mean degree after normalisation')
ax[0,2].plot(T, L_max_degree_2, label='Max degree after normalisation')
ax[1,0].plot(T, L_density_2, label='After normalisation')
ax[1,1].plot(T, L_transitivity_2, label='After normalisation')
ax[1,2].plot(T, L_modularity_2, label='After normalisation')
ax[2,0].plot(T, L_diameter_2, label='After normalisation')
ax[2,1].plot(T, L_ASPL_2, label='After normalisation')
ax[2,2].plot(T, L_mean_viewer_2, label='Mean # of viewers after normalisation')
ax[2,2].plot(T, L_max_viewer_2, label='Max # of viewers after normalisation')
#Graphs
ax[0,0].set_ylabel('# of edges')
ax[0,1].set_ylabel('# of nodes')
ax[0,2].set_ylabel('Degree')
ax[1,0].set_ylabel('Density')
ax[1,1].set_ylabel('Transivity')
ax[1,2].set_ylabel('Modularity')
ax[2,0].set_ylabel('Diameter')
ax[2,1].set_ylabel('Average shortest path length')
ax[2,2].set_ylabel('# of viewers')
ax[0,0].set_yscale('log')
ax[0,0].legend()
ax[0,1].legend()
ax[0,2].legend()
ax[1,0].legend()
ax[1,1].legend()
ax[1,2].legend()
ax[2,0].legend()
ax[2,1].legend()
ax[2,2].legend()
ax[2,0].set_xlabel('Temps (h)')
ax[2,1].set_xlabel('Temps (h)')
ax[2,2].set_xlabel('Temps (h)')
plt.show()
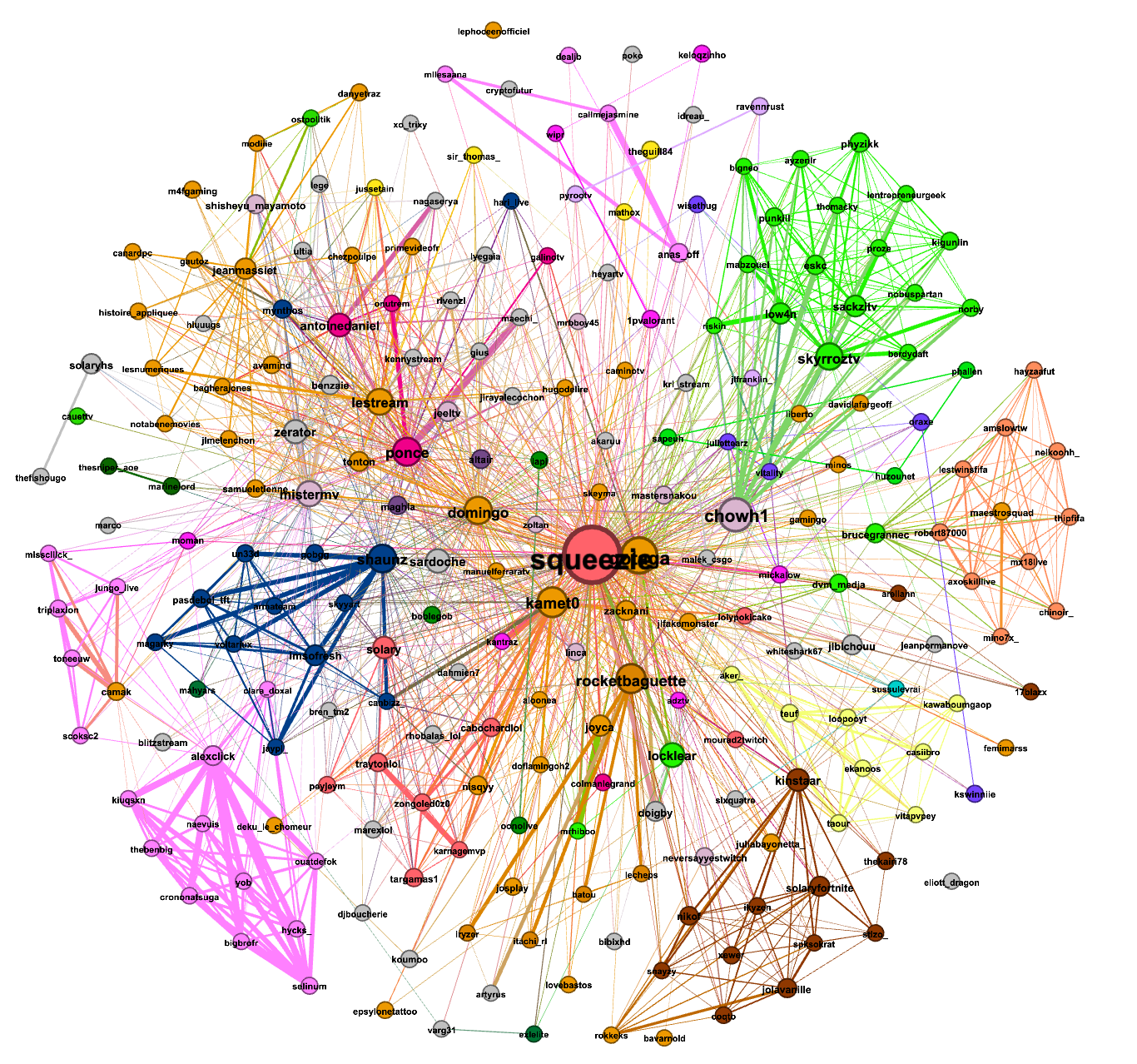

 The first graph was made from the data gathered from (Sunday)12/12/2021-15h37 to 13/12/2021-15h22:
The first graph was made from the data gathered from (Sunday)12/12/2021-15h37 to 13/12/2021-15h22:
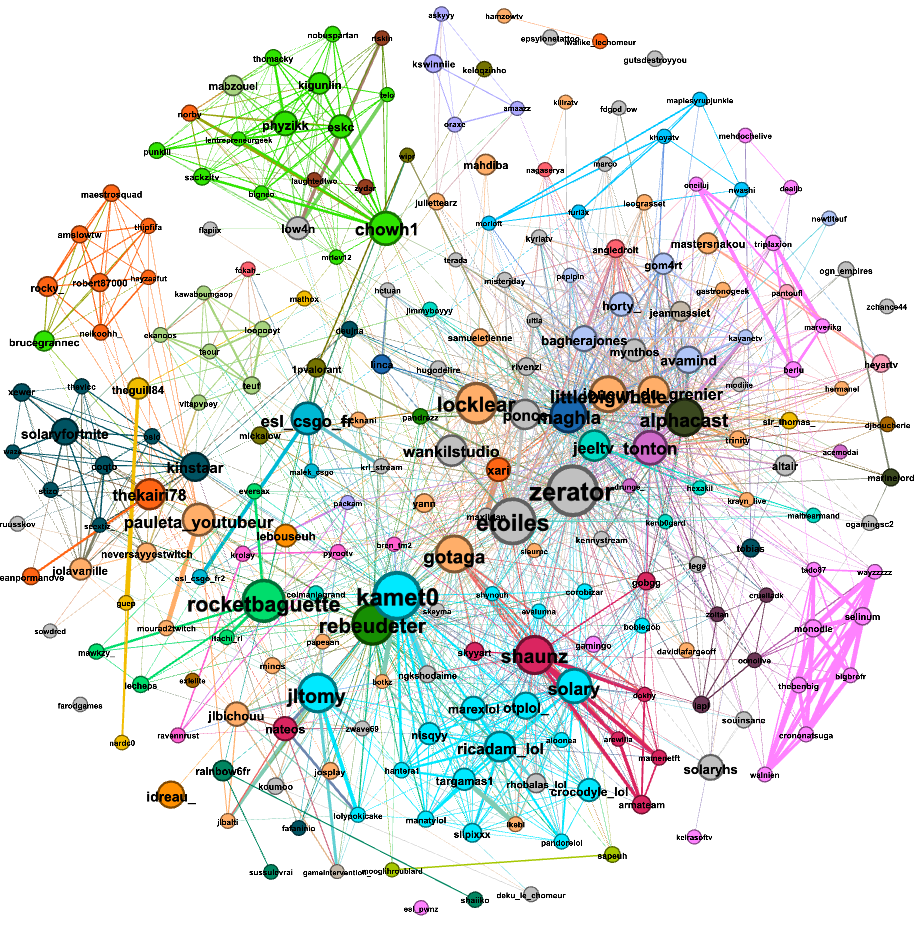 The first graph was made from the data gathered from (Monday)13/12/2021-15h37 to 14/12/2021-15h22:
The first graph was made from the data gathered from (Monday)13/12/2021-15h37 to 14/12/2021-15h22:
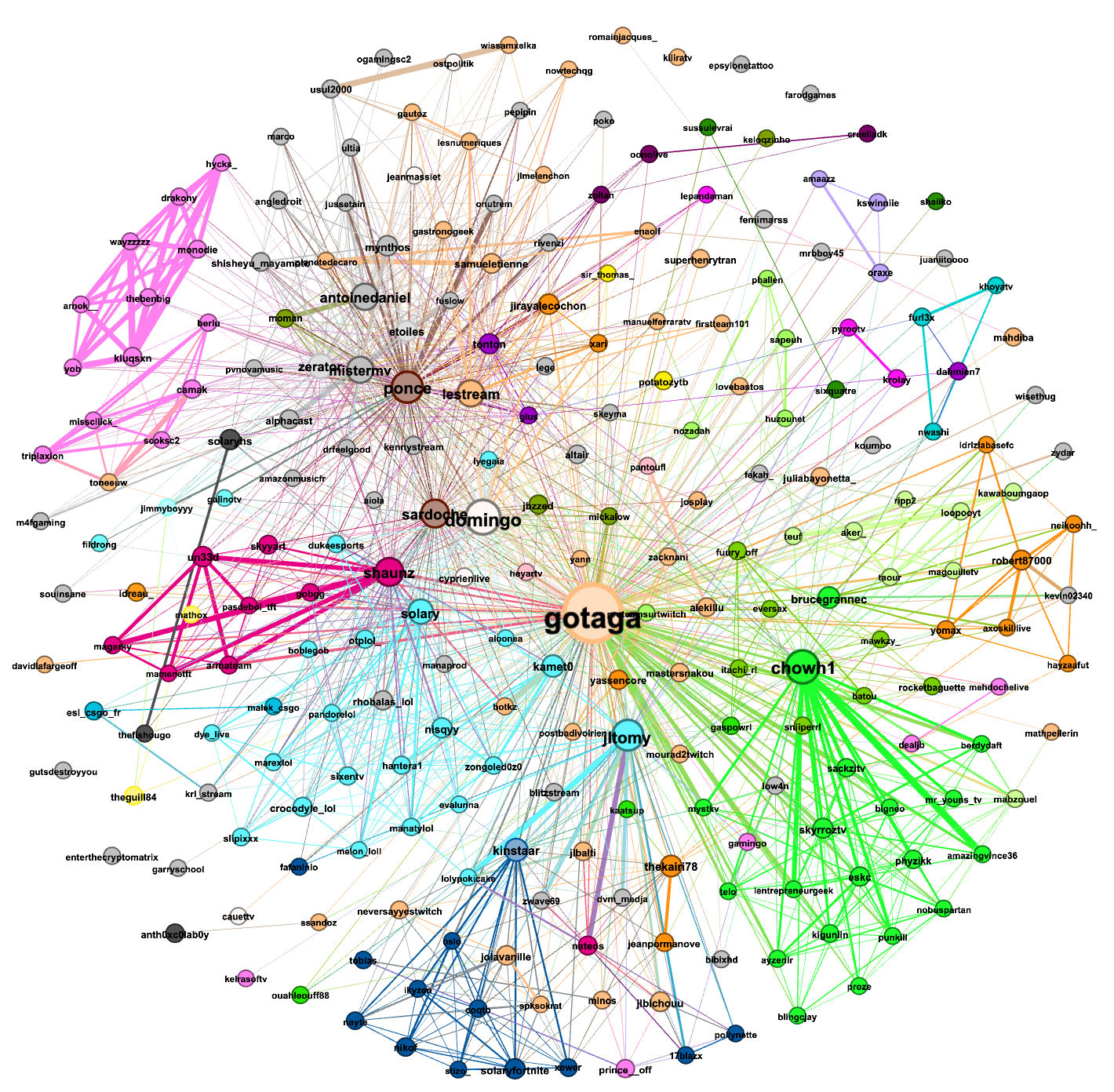 The first graph was made from the data gathered from (Tuesday)14/12/2021-15h37 to 15/12/2021-15h22:
The first graph was made from the data gathered from (Tuesday)14/12/2021-15h37 to 15/12/2021-15h22:
